Dinamic Programming(다이나믹 프로그래밍) 이란?

Dinamic Programming(다이나믹 프로그래밍) 이란?

한국말로 동적계획법 이라고 한다.

동적 계획법은 분할 정복과 같은 접근 방식을 가지고 있다.

큰 문제를 작은 문제로 나누어서 각각의 답을 계산하고, 이 답들로부터 원래 문제에 대한 답을 계산해 내기 때문이다.

동적 계획법에서 어떤 부분 문제는 두 개 이상의 문제를 푸는데 사용될 수 있기 때문에, 이 문제의 답을 메모리에 저장해 둘 필요가 있다.

이 때 이미 계산한 값을 저장해 두는 메모리의 장소를 캐시(cache)라고 부르고, 두 번 이상 계산되는 부분 문제를 중복되는 부분 문제(overlapping subproblems)라고 부른다.

중복되는 부분문제의 예시

(a)

(b)

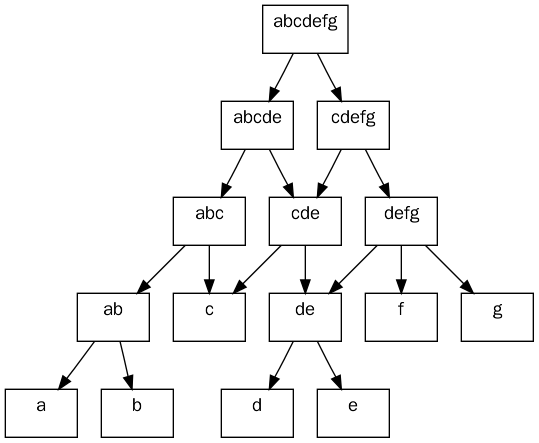
(a) : 각 문제들이 서로 연관이 없기 때문에, 단순하게 재귀 호출을 통해 문제를 분할해도 한 부분 문제를 한번만 해결하게 된다.

(b) : 나눠진 각 문제들이 같은 부분 문제에 의존한다

(b)의 경우에는 분할의 깊이가 깊어질 수록 계산의 중복 횟수가 지수적으로 증가하게 된다. 이런 문제를 해결하기 위해 고안된 알고리즘 설계 기법이 바로 동적 계획법이다.

동적 계획법의 대표적인 예시에는 이항 계수(binomial coefficient가 있다.

• nCr : n개의 서로 다른 원소 중에서 r개의 원소를 순서없이 골라내는 방법의 수

\[ {n\choose r} = {n-1\choose r-1} + {n-1\choose r} \]

이항 계수 nCr 에 대해서 위 식이 성립한다.

이것을 코드로 나타내면 다음과 같다.

int bino(int n, int r){
	if(r == 0 || n == r) return 1;
	return bino(n-1, r-1) + bino(n-1, r);
}

이항계수의 과도한 중복계산

그런데, 이렇게 코드를 짜게되면 중복되는 부분이 많이 생기기 때문에 가장 작은 (1,0) 이나 (1,1)같은 경우 깊이가 증가할 수록 거의 지수함수꼴로 호출되는 횟수가 증가한다.

심지어 (25,12)인 경우에는 함수의 호출횟수가 1000만번이 넘게된다.

이런 계산량의 낭비는 피할 수 없을까?

중복 계산 제거 방법

입력인 n과 r이 정해져 있을 때, bino(n, r)의 반환 값이 일정하다는 사실을 이용하면, 중복 계산을 제거할 수 있다.

각 bino(n,r)에 대해 답을 저장하는 캐시 배열을 만들어서 반환값을 저장하면 된다.

만약에 계산되어 있지 않은 경우에는 직접 계산해서 배열에 넣고 반환하면 되고, 계산되어 있으면 배열에 접근해서 즉시 반환하면 된다.

이와 같이 함수의 결과를 저장하는 장소를 마련해두고, 한 번 계산한 값을 저장해 뒀다 재활용하는 최적화 기법을 메모이제이션(memoization)이라고부른다.

메모이제이션을 이용한 이항 계수의 계산을 코드로 나타내면 다음과 같다.

메모이제이션을 적용한 이항계수

int cache[30][30];
int bino2(int n, int r){
	if(r == 0 || n == r) return 1;
	int& ret = cache[n][r]; 
	if(ret == -1){
		return ret = bino2(n-1, r-1) + bino2(n-1, r);
	}
	return ret;
}

bino2 함수는 (25,12)인 경우에 호출횟수가 181번 밖에 안된다.

즉, DP는 overlapping subproblems에
memoization을 적용함으로써 속도의 향상을 꾀하는
알고리즘 설계 기법이다.