Cambricon: An Instruction Set Architecture for Neural Networks
0. Abstract
Neural Networks(NN)은 광범위한 새로운 machine leanring과 패턴 인식 application들을 위한 모델 집합이다.
NN 테크닉들은 일반적으로 general-purpose processors(cpu, gpgpu)에서 실행되는데, 이것들은 다양한 workload를 유연하게 지원하기 위해 hardware resource들을 지나치게 투자할 때 보통 에너지 효율적이지 않다.
따라서, NN을 위한 application-specific한 hardware accelerator들이 에너지 효율성을 개선하기 위해 최근에 제안됐다.
그러나 그런 acclerator들은 유사한 계산 패턴을 공유하는 NN 테크닉들의 극히 일부분을 위해 디자인되었고, 그들은 NN의 고수준 functional block(layer) 또는 심지어 NN 전체에 직접 대응되는 복잡하고 정보량이 많은 instruction들을 채택하였다.
비록 비슷한 NN 테크닉에서의 제한된 set에서 간단하고 구현하기 쉽지만, instruction set 에서의 민첩성 부족은 다양한 NN 테크닉의 효율성과 충분한 유연성을 지원하기 위한 accelerators 디자인을 만들기 어렵게 한다.
이 논문에서는 존재하는 NN technique들의 포괄적인 분석을 기반으로 scalar,vector,matrix,logical,data transfer, control instruction을 통합하고 load-store architecture를 사용한 Cambricon이라고 불리는 NN accelerator들의 새로운 domain-specific ISA를 제안한다.
cambricon에 다양한 NN technique들에 대해서 수용력이 있다는 것을 10개가 넘는 대표적인 넘는 서로 다른 NN technique들의 실험을 통해 증명하고 MIPS, GPGPU, x86과 같은 general-purpose ISA보다 높은 code density를 제공하는 것도 보인다.
최근 DaDianNao(3가지 NN 테크닉을 지원)과 Cambricon-based accelerator와 비교한다.
Cambricon ISA는 다른 NN accelerator들의 ISA와는 다르게 다양한 NN 테크닉들을 지원하고, 기존 범용 ISA보다 높은 code density를 제공한다(성능이 좋다)
1. Introduction
NN은 뇌과학에서 영감을 얻어 시작된 아주 큰 범위의 machine learning 기술이고 최근 10년넘게 깊고 크게 발전해왔다.
비록 NN이 계산 비용이 많이 들지만, 그 중 일부는 특정 작업에서 인간의 수준의 성능을 달성하였다.
원래 NN 테크닉은 CPU와 GPGPU로 구성된 gerneral purpose platform으로 실행되었다.
이 CPU와 GPGPU 모두 다양한 workload를 유연하게 지원하기 위해 hardware resource를 과도하게 투자하기 때문에 에너지 효율성이 떨어진다.
에너지 효율성을 높이기 위해 최근 NN에 맞춤화된 hardware accelerator들이 연구되고 있다.
이러한 hardware acclerator들은 낮은 수준의 작업(dot-product)이 아닌 높은 수준의 layer(convolution, pooling, classifier) 또는 NN전체에 해당하는 고수준 그리고 infomative instruction들을 도입하였고, 그들의 decoder들은 각 instruction에 fully optimized 될 수 있다.
비록 유사한 NN 기술의 작은 set(small instruction set)에 대해 간단하고 구현하기 쉽지만, 다양한 NN 기술을 유연하게 지원해야 할 필요성이 instruction set의 상당한 확장을 초래할 때, 그러한 accelerator에 대한 디코더의 설계 검증 복잡성과 면적/전력 오버헤드는 받아들일 수 없을 정도까지 쉽게 커진다.
결과적으로, 이러한 acclerator들은 매우 유사한 계산 패턴과 data locality를 공유하는 NN 테크닉의 작은 subset에서만 효율적으로 지원할 수 있고, 기존 NN 기술간의 다양성을 처리할 수 없다.
예를들어 SOTA NN가속기인 DadiaNao는 MLP를 효율적으로 처리할 수 있지만, 뉴런들이 각각 fully connected 된 BM은 수용할 수 없다.
결과적으로 ISA 설계는 현존하는 NN acclerator들의 유연성과 효율성을 크게 제한하는 지금까지 미해결된 근본적인 과제이다.
범용 ISA(CPU, GPGPU)는 에너지 효율성이 떨어져서 NN accelerator들이 나왔지만, 유연성과 효율성이 부족하다.
이 논문에서는 RISC ISA 설계 원리에 영감을 받아 NN accelerator의 ISA를 설계하였다.
NN의 고수준 functional block(layer)들을 설명하는 복잡하고 정보가 많은 instruction들을 저수준 계산 작업(dot product)에 해당하는 짧은 instruction으로 분리하면 사용자가 이제 저수준의 작업을 사용하여 새로운 NN 테크닉에 필수적인 새로운 고수준의 functional block을 조합할 수 있으므로 가속기가 더 넓은 응용 범위를 가질 수 있다.
기존에는 고수준에 맞는 instruction들을 도입하였지만, 이 논문에서 제시하는 ISA는 dot product와 같은 저수준의 instruction을 사용하여 고수준의 block을 조합할 수 있으므로 유연성을 해결할 수 있다.
이렇게 설계한 ISA를 Cambricon으로 명명하였다. Cambricon은 instruction은 모두 64bit인 load-store 아키텍쳐를 사용하였고, 주로 control 및 address 지정 목적을 위해 스칼라를 위한 64 32bit의 General-Purpose Registers(GPRs)를 사용하였다.
영역, 전력 오버헤드가 거의 없는 vertor, matrix data에 대한 집중적이고 지속적인 가변 길이의 접근을 지원하기 위해서, Cambricon은 vector register file을 사용하지 않고 data를 프로그래머와 컴파일러에게 visible한 on-chip scratchpad memory에 저장한다.
주소의 하위 비트로 분해된 서로 다른 뱅크에 대한 동시 액세스는 NN 기술을 지원하기에 충분하기 때문에 on-chip 메모리에 여러 포트를 구현할 필요가 없다.
register file의 제한된 폭에 의해 성능이 제한되는 SIMD와 달리 캠브리콘은 on-chip scratchpad memory의 뱅크를 register file보다 쉽게 넓힐 수 있기 때문에 더 크고 가변적인 데이터 width를 효율적으로 지원한다.
vector, matrix data에 대한 지속적인 가변적인 길이의 접근을 위해 data를 register file에 저장하지 않고, register file보다 뱅크를 쉽게 넓힐 수 있는 on-chip scratchpad memory에 저장한다.
10개의 대표적인 NN 테크닉(MLP, CNN, RNN, LSTM, AE, SAE, BM, RBM, SOM, HNN)으로 Cambricon을 평가하였다. 그 결과 MIPS보다 13.9배, x86보다 9.86배, GPGPU보다 6.41배의 code density, 최신 NN accerlerator 설계인 DaDianNao와 비교하면 무시할 수 있는 latency, power, area overhead(4.5%, 4.4%, 1.6%)가 발생한다.
범용 ISA보다 훨씬 나은 성능을 보여주고, NN accelerator DaDianNao와는 거의 비슷한 성능을 보여주지만 DaDianNao는 3가지 NN 테크닉만을 지원하기 때문에 Cambricon이 더 유연하다.
이 논문의 핵심 의의는 다음과 같다.
- 다양한 NN 테크닉들에 대해 수용력을 가진 새롭고 가벼운 ISA를 제안한다.
- 기존 NN 기술 연구의 계산 패턴에 대한 포괄적인 연구를 수행한다.
- TSMC 65nm 기술로 구현한다.
이 논문의 나머지부분은 다음과 같다.
Section 2 : Cambricon을 따르는 설계 가이드라인과 overview를 제시
Section 3 : Cambricon의 computational and logical instruction을 소개
Section 4 : Cambricon accelerator의 프로토타입
Section 5 : 다른 ISA들과의 성능 비교
Section 6 : Cambricon의 확장 잠재력에 대한 논의
2. Overview of The Proposed ISA
이 섹션에서는 논문에서 제안한 ISA에 대한 설계 가이드라인 및 ISA 개요에 대해 설명한다.
A. Design Guidelines
NN을 위한 간결, 유연, 효율적인 ISA를 설계하기 위해서 우리는 구체적인 설계 결정을 내리기 전에 몇 가지 설계 가이드라인을 기반으로 다양한 NN 테크닉들을 그들의 계산 operation과 메모리 액세스 패턴의 측면에서 분석하였다.
Data-level Parallelism(DLP)
대부분의 NN 테크닉들이 뉴런과 시냅스 데이터들이 layer들로 구성된 다음 균일하고 대칭적인 방식으로 조작된다는 것을 알아냈다.
이러한 연산을 이용할 때 vector/matrix instruction들로 지원되는 DLP가 전통적인 scalar instruction의 ILP보다 더 효율적이고, 더 높은 코드 밀도를 가질 수 있다.
Customized Vector/Matrix Instructions
많은 선형대수 라이브러리(e.g., BLAS 라이브러리)가 존재하지만, NN 테크닉의 경우 선형대수 라이브러리에 정의된 기본 operation들이 꼭 효과적이고 효율적인 선택은 아니다.
더 중요한 점은, 많은 공통적인 NN 테크닉의 operation들은 전통적인 선형대수 라이브러리에서 다루지 않는 것들이 많다.
예를들면 BLAS 라이브러리는 벡터의 요소별 지수 계산을 지원하지 않고, 시냅스 초기화, 드롭아웃, Restricted Boltzmann Machine(RBM)의 random vector 생성도 지원하지 않는다.
따라서 기존 선형 대수 라이브러리에서 단순히 vector/matrix 연산을 다시 구현하는 대신 기존 NN 기술에 대해 작지만 대표적인 vector/matrix instruction의 set을 철저하게 customize해야만 한다.
Using On-chip Scratchpad Memory
NN 테크닉들이 vector/matrix 데이터에 대한 집중적이고 연속적인 가변 길이의 access가 자주 요구된다는 것을 발견하였다.
그렇기에 고정 길이의 vector register file들은 더이상 cost-effective한 선택이 아니게 됐다.
우리의 설계에서 이 vector register file들을 각 데이터 access에 유연한 길이를 제공하는 on-chip scratchpad memory로 대체하였다.
Data-level Parallelism(DLP)를 사용하고, 기존 선형대수 라이브러리를 사용하지 않고 custom 한 instruction set을 사용하고, on-chip scratchpad memory를 사용한다.
B. An Overview to Cambricon
Cambricon은 load/store instruction으로 main memory에 access하게 허용하는 load-store 아키텍쳐이다.
Cambricon은 scalars를 위한 64 32bit의 GPRs를 포함한다. 이는 on-chip scratchpad memory의 register-indirect addressing에 사용될 뿐만 아니라 scalar data를 임시로 보관하는 용도로도 사용된다.
Type of Instructions
Cambricon은 4가지 타입의 instruction을 포함한다.
- computational
- logical
- control
- data transfer
비록 다른 instruction들끼리는 valid bit들의 수가 다르겠지만, instruction의 길이는 memory-alignment를 위하여, 또 load/store/decoding 과정을 간단하게 설계하기 위해 64bit로 고정되어있다.
이 섹션에서 control(jump, branch)과 data transfer(load/store/move) instruction에 대해서는 비록 NN 테크닉에 맞게 조정되었지만 MIPS instruction들과 유사하기 때문에 간결하게 설명한다.
computational instruction과 logical instruction들(matrix, vector, scalar instruction을 포함하는)에 대해서는 다음섹션(3장)에서 설명한다.
Control Instructions
캠브리콘에는 2가지 control instruction인 jump 와 conditional branch가 존재한다.
jump instruction은 PC에 더해질 값인 immediate값 또는 GPR 값을 통해 offset을 지정한다.
conditional branch는 0과 predictor(GPR에 저장되어있는)를 비교하여, branch의 타겟을 PC+1로 정할지, PC+{offset}으로 할지 결정한다.
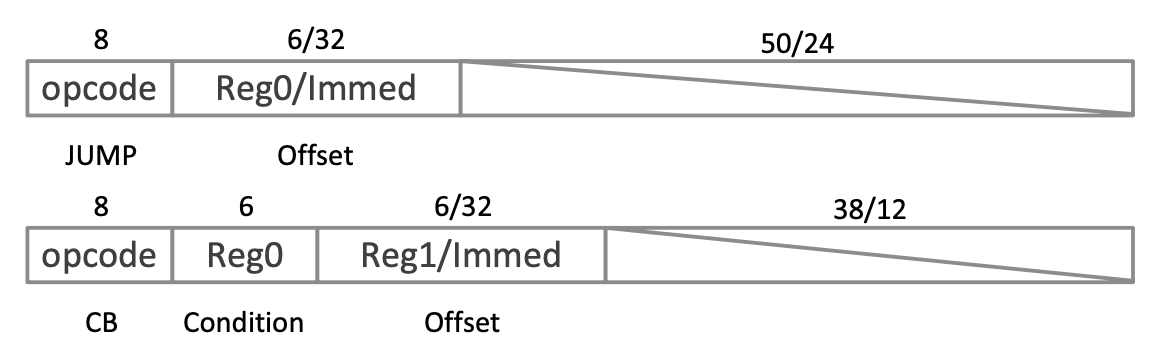
Data Transfer Instructinos
Cambricon의 Data transfer instruction은 유연하게 matrix, vector computational/logical instruction을 지원하기 위해서 가변 길이의 data를 지원한다.
이 instruction들은 main memory → on-chip scratchpad, on-chip scratchpad → scalar GPRs variable-size data block을 load/store 할 수 있다.
VLOAD(vector load) instruction은 $V_{size}$ 크기 만큼의 vector를 main memory에서 vector scratchpad memory로 불러온다.
main memory안의 source address는 GPR에 저장되어있는 base address와 immediate 값을 더하면 된다.
VSTORE, MLOAD, MSTORE 모두 VLOAD와 유사하다.

On-chip Scratchpad Memory
Cambricon은 vector register file을 사용하지 않는 대신 programmer/compiler에게 visible하게 만들어진 on-chip scratchpad에 데이터를 직접 보관한다.
다시말해, 전통적인 ISA들의 vector register file과 Cambricon의 scratchpad memory의 역할이 비슷하고, vector 피연산자의 크기가 더 이상 고정길이 vector register file에 의해 제한되지 않는다는 것이다.
그러므로, vector/matrix 크기는 Cambricon instruction에 의해 변하게 되고, 다만 한가지 주목할만한 제한점은 동일한 instruction 내부의 vector/matrix 피연산자가 scratchpad memory의 용량을 초과할 수 없다는 점이다.
만약 초과한다면, compiler는 긴 vector/matrix를 짧은 조각 및 블록으로 분해하고 여러개의 instruction을 만들어 처리한다.
32x512b 벡터 레지스터가 Intel AVX-512에 구워진 것 처럼 vector/matrix instruction을 위한 on-chip memory의 용량도 고정되어야 한다.
더 상세하게 말핮면, Cambricon의 memory 용량은 vector instruction에 대해서는 64KB로 고정되고, matrix instruction에 대해서는 768KB로 고정된다.
그렇지만, Cambricon은 scratchpad memory의 bank 갯수에 대해서는 특별한 제한을 두지 않아서, microarchitecture-level 구현에 상당한 자유를 준다.
Cambricon은 4가지 타입의 instruction으로 구성되어있고, 이 중 control과 data transfer instruction은 기존 MIPS의 구조와 비슷하다. 또한, on-chip scratchpad memory를 사용함으로써 가변길이에서의 장점이 있다.
3. Computational/Logical instructions
NN에서 대부분의 operation(addition, multiplication, activation function들)은 vector operation으로 모여 나타낼 수 있으며, 그 비율은 99.992%까지 높아 질 수 있다.
즉, NN은 scalar, vector, matrix 연산으로 자연스럽게 분해될 수 있으며, ISA는 DLP와 data locality를 극대화할 수 있도록 설계되어야 한다.
A. Matrix Instructions
존재하는 NN 테크닉들에 대해 철저하고 포괄적인 분석을 하였고, Cambricon을 위한 총 6개의 matrix instruction을 설계하였다.
NN중 MLP를 사용하여 matrix instruction이 어떻게 지원되는지 보여줄 것이다.
기술적으로 MLP는 보통 multiple layer들을 가지고, 각 layer는 Input 뉴런에 따라 output 뉴런을 계산한다.
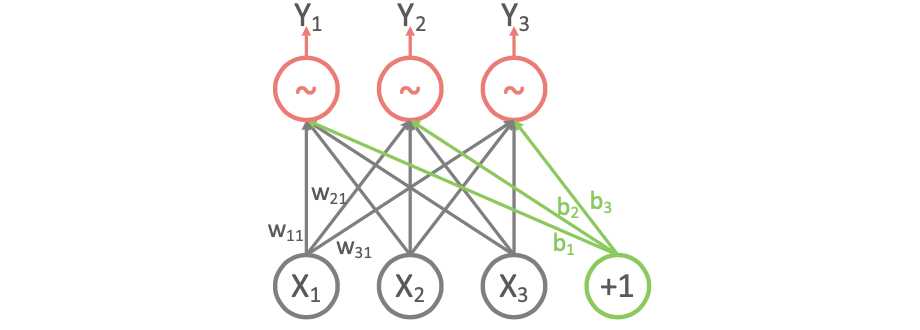
output 뉴런인 $y_i\space(i = 1,2,3)$ 은 $y_i = f(\Sigma_{j=1}^{3} w_{ij}x_{j}+b_i)$와 같이 계산된다.
$x_j$는 input 뉴런
$w_{ij}$는 i번째 output 뉴런과 j번째 input 뉴런의 weight
$b_i$는 i번째 아웃풋 뉴런의 bias
$f$는 activation function
그래서 output 뉴런은 vector $y = (y_1, y_2, y_3)$에 대해 다음과 같이 나타낼 수 있다.
\[y = f(Wx+b)\]$x = (x_1, x_2, x_3)$이고, $b = (b_1, b_2, b_3)$인 input 뉴런과 bias vector이다.
$W = (w_{ij})$인 weight matrix이고, $f$는 activation function의 요소별 버전이다.
위의 식에서 $Wx$를 계산할 때, Cambricon의 Matrix-Mult-Vector(MMV)에 의해 수행된다.
MMV instruction은 아래 그림과 같다.

Reg0 : vector output의 scratchpad memory base address
Reg1 : vector output size
Reg2 : matrix input의 base address
Reg3 : vector input의 base address
Reg4 : vector input의 size
→ matrix에 vector를 곱하면 vector 형태로 나오므로 vector는 input, output이 모두 존재하고, matrix는 Input만 존재한다.
MMV instruction은 모든 input, output 데이터를 scratchpad memory에 동시에 보관할 수 있는 한 임의의 scale에서 matrix-vector 곱셈을 지원할 수 있다.
$Wx$를 여러개의 vector dot 연산으로 분해하는 대신, MMV instruction을 사용해서 계산할 수 있다. 여러개의 vector dot 연산으로 바꾸어버리면 input vector $x$를 재사용하기 위해 추가적인 노력이 필요하다. (explicit synchronization, 같은 address를 요청하였을 때 동시 읽고 쓰기 문제)
위와 같은 feedforward와는 다르게, MMV instruction이 더이상 NN의 backforward training에는 효율적으로 제공되지 않는다.
더 자세하게는 Back-Propagation(BP)알고리즘은 gradient vector를 계산해야 한다.
이것을 MMV instruction으로 구현하려면 추가적으로 matrix transpose를 구현하는 instruction이 필요하다. 그리고 이것은 데이터 흐름에서 더 많은 비용을 필요로 한다.
이것을 피하기 위해서, Cambricon은 backforward training에 적용되는 Vector-Mult-Matrix(VMM) instruction을 제공한다. VMM instruction은 opcode를 제외하고 MMV와 비슷한 filed들을 제공한다.
게다가 NN training 과정에서 weight matrix $W$는 $W = W + \eta\Delta W$로 업데이트 된다.
여기서 $\eta$는 learning rate(스칼라)이고, $\Delta W$는 두 vector의 outer product로 계산된다.
그렇기에 Cambricon은 output이 matrix인 Outer-Product(OP) instruction과 Matrix-Mult-Scalar(MMS) instruction, Matrix-Add-Matrix(MAM) instruction을 모두 weight update를 수행할 때 제공한다.
그리고 RBM에서 weight update를 위한 Matrix-Subtract-Matrix(MSM) instruction 또한 제공된다.
NN 테크닉에서 matrix에 관련된 연산을 많이 수행하는데, 그것을 지원하기 위해 MMV instruction을 제공한다. 그러나 이것은 forward 과정에서 수행되는 것이고, backpropagation 과정을 위해 VMM, MMS, MAM, MSM, OP 등의 instruction도 지원한다.
B. Vector instruction
matrix instruction 만으로는 모든 계산을 수행하기에 불충분하다. $Wx + b$와 같은 bias vector를 더하는 연산을 하였을 때, vector add instruction이 필요하다.
Cambricon은 Vector-Add-Vecvor(VAV) instruction을 vector addition을 위해 제공하지만, 요소별 activation을 지원하기 위해 여러개의 instruction이 필요하다.
일반성을 잃지 않기 위해 아주 넓게 쓰이는 sigmoid activation function인 $f(a) = e^a/(1+e^a)$를 예시로 들었다.
input vector 의 각 요소에 대해 수행되는 요소별 sigmoid activation은 3가지 연속적인 step으로 분해되고, 각각 3가지 instruction에 의해 지원된다.
- 인풋 벡터 a에 대해 각 element($a_i,i=1,\dots,n$ )의 exponential $e^{ai}$를 계산하기 위해 Cambricon은 벡터의 요소별 exponential을 위한 Vector-Exponential(VEXP) instruction을 제공한다.
- 상수 1과 각 벡터의 요소를 더하기 위해($e^{a1},\dots,e^{a_n}$) Cambricon은 Vector-Add-Scalar(VAS) instruction을 제공한다. 이 때, Scalar는 immediate 또는 GPR에 의해 특정되는 값이 된다.
- $e^{a_i}$를 $1+e^{a_i}$로 나누기 위해, Cambricon은 서로 다른 벡터에서 요소별 division을 위한 Vector-Div-Vector(VDV) instruction을 제공한다.
그러나, sigmoid는 NN의 유일한 activation function이 아니므로, 다양한 activation function의 요소별 버전을 구현하기 위해, Cambricon은 Vector-Mult-Vector(VMV), Vector-Sub-Vector(VSV), Vector-Logarithm(VLOG)을 제공한다.
→ 이는 vector arithmetic instruction이다.
hardware accelerator 설계 중에 서로 다른 초월함수(e.g., 로그, 삼각함수 및 반삼각함수)와 관련된 instruction은 CORDIC 기법을 사용하여 동일한 functional block(추가, 시프트 및 테이블 룩업 연산 포함)을 효율적으로 재사용할 수 있다.
또한 논리 연산(e.g., 비교)에 부분적으로 의존하는 활성화 함수(예: max(0,a) 및 |a|)가 있으며, 섹션 III-C에서 관련 Cambricon isntruction(e,g., vector compare instructions)을 제시할 것이다.
게다가, random vector generation은 수많은 NN 테크닉들(e.g., dropout, random sampling)에서의 중요한 operation이다. 그러나 scientific computing을 위해 설계된 선형대수 library에서는 필수가 아니라고 생각한다.(e.g., BLAS는 random vector generation이 없다.)
Cambricon은 [0,1] 사이의 uniform 분포를 따르는 random number의 vector를 생성하는 전용 instruction(Random-Vector, RV)을 제공한다.
주어진 random vector들로 vector compare instruction과 vector arithmetic instruction의 도움을 받아 Ziggurat 알고리즘을 사용하여 gaussian distribution과 같은 다른 분포들을 생성할 수 있다.
Matrix instruction 말고도 vector의 arithmetic 연산을 위해 Vector instruction이 제공된다. 그 예로는 VLOG, VEXP, VAV, VDV, VMV, VSV, VAS instruction이 있다. 또한 vector compare instruction, random-vector instruction 등을 제공한다. 이것들로 많은 NN 테크닉의 activation function 및 여러가지 분포를 만들어 낼 수 있다.
C. Logical Instructions
SOTA NN 테크닉들은 logical, comparison 조작을 포함하는 몇가지 operation을 활용한다.
max-pooling operation은 아래 그림과 같이 pooling window 안에서 가장 큰 output을 가지는 뉴런을 찾고, 다른 feature map에서 이러한 행동을 반복하는 작업이다.
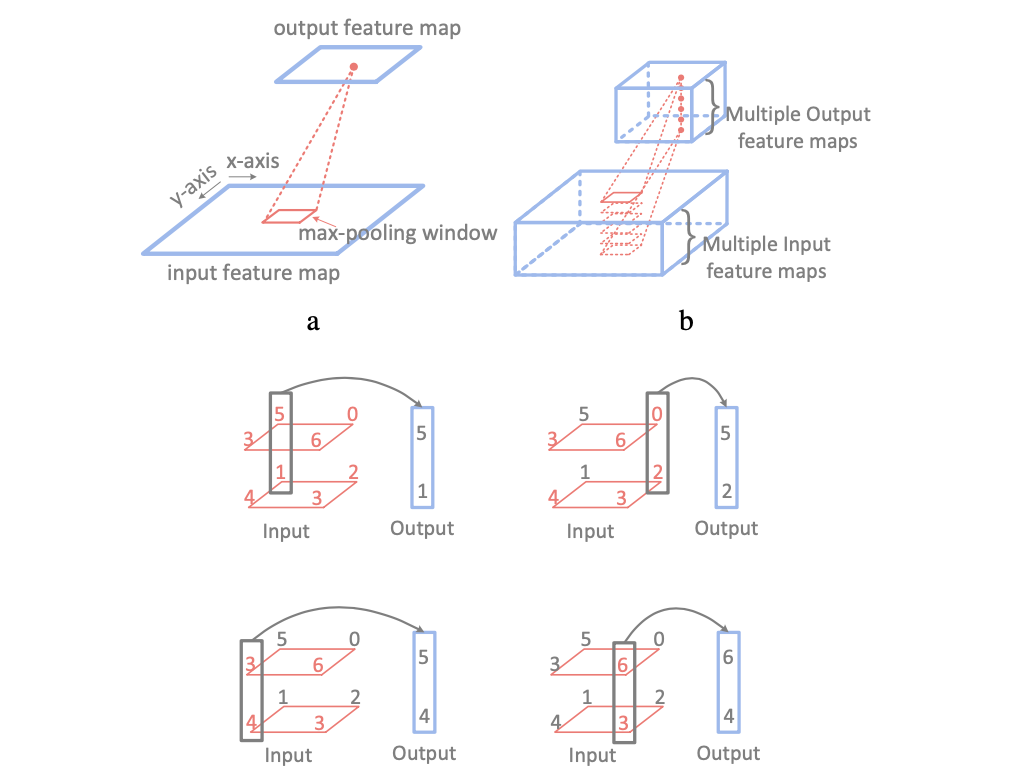
Cambricon은 Vector-Greater-Than-Merge(VGTM) instruction을 사용하여 max-pooling operation을 지원한다. 이 VGTM instruction의 구조는 아래와 같다.